Flow to rivers and the hydrograph

Water flowing through a catchment produces discharge in its rivers.

Learning Goals

• Know (and review) how water moves through a catchment, with a focus on its journey towards a river.
• Understand how a rainfall hyetograph can produce a discharge hydrograph.
• Know the definition of river discharge and its relationship both to mass balance through a watershed and flow through a channel.

River discharge

River discharge is the sum of all water inputs (precipitation, groundwater exfiltration, snowmelt) and outputs (evapotranspiration, groundwater infiltration, snow/ice storage) that have occurred in the catchment feeding a particular point along a river. Such a point, for example, could occur somewhere in the basin below. If this point is at the outlet of the basin, it is equal to the \(Q\) shown at the right:

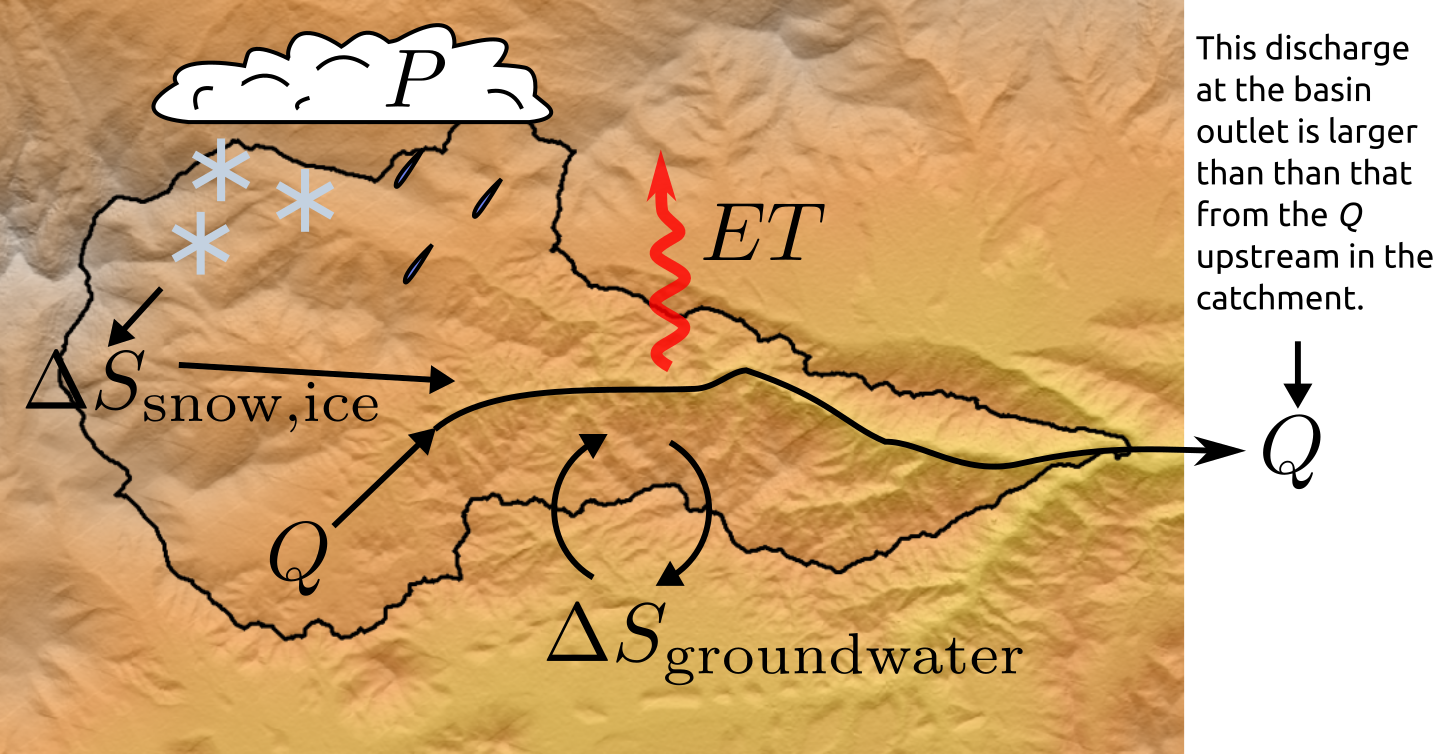
Diagram by Andy Wickert

Recall that in a time-averaged sense that river discharge can be given by:

\[Q = P - ET - \Delta S\]

where \(Q\) is river discharge, \(P\) is precipitation, \(ET\) is evapotranspiration, and \(\Delta S\) is change in storage within the watershed (e.g., in groundwater or snowpack. Recall that all of these input values are summed across the entire area ($A$) of the drainage basin (= catchment, = watershed) draining to the point of interest (e.g., where there is a stream gauge that can measure discharge).

Within the physical stream, river discharge can be defined as the mean velocity of the flow traveling through a cross section of river times the cross-sectional area of the river:

• Figure from Penn State e-education*

Terms and variables:

• River width: $b$ (breadth; thanks, England!)
• River depth: $h$ (height of flow)
• Mean flow velocity: $\bar{u}$
• Cross-sectional area: $A_c$

From this, we can define discharge as:

\[Q = \bar{u} A_c\]

For simplicity, we often assume that river channels are approximately rectangular in cross section. This approximation quite often isn’t as terrible as one might think: many rivers are ~20x as wide as they are deep, meaning that any variations in depth are quite subtle. Of course, this approximation is not used when precisely gauging the stream discharge, but it can be good enough for work to understand geomorphology.

\(A \approx b h\),

and therefore,

\(Q \approx \bar{u} b h\).

Videos

Water flow to rivers

Here, I quickly recap the major ways that water moves from the catchment into the river channel, contributing to discharge.

Precipitation to river discharge: the hydrograph

This first video from The Geographysical quickly goes through the main concepts that I hit in a way that is much more smoothly produced!

This is the video of my lecture, which goes a bit more slowly and in depth on processes that connect precipitation and flow within the watershed to river discharge:

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.